our libraryhere every speaker is welcome to contribute with a couple of interesting references |
|---|
-
 Fitting smooth functions to dataCharles Fefferman, and Arie Israel2020
Fitting smooth functions to dataCharles Fefferman, and Arie Israel2020This book is an introductory text that charts the recent developments in the area of Whitney-type extension problems and the mathematical aspects of interpolation of data. It provides a detailed tour of a new and active area of mathematical research. In each section, the authors focus on a different key insight in the theory. The book motivates the more technical aspects of the theory through a set of illustrative examples. The results include the solution of Whitney’s problem, an efficient algorithm for a finite version, and analogues for Hölder and Sobolev spaces in place of Cm. The target audience consists of graduate students and junior faculty in mathematics and computer science who are familiar with point set topology, as well as measure and integration theory. The book is based on lectures presented at the CBMS regional workshop held at the University of Texas at Austin in the summer of 2019.
-
 Reconstructing a neural net from its outputCharles FeffermanRev. Mat. Iberoamericana, 1994
Reconstructing a neural net from its outputCharles FeffermanRev. Mat. Iberoamericana, 1994Neural nets were originally introduced as highly simplified systems of the neural system. Today they are widely used in technology and studied theoretically by scientists from several disciplines. (See e.g. [N]). However they remain little understood. (...)
-
 The Dimpled Manifold Model of Adversarial Examples in Machine LearningAdi Shamir, Odelia Melamed, and Oriel BenShmuel2022
The Dimpled Manifold Model of Adversarial Examples in Machine LearningAdi Shamir, Odelia Melamed, and Oriel BenShmuel2022The extreme fragility of deep neural networks, when presented with tiny perturbations in their inputs, was independently discovered by several research groups in 2013. However, despite enormous effort, these adversarial examples remained a counterintuitive phenomenon with no simple testable explanation. In this paper, we introduce a new conceptual framework for how the decision boundary between classes evolves during training, which we call the \em Dimpled Manifold Model. In particular, we demonstrate that training is divided into two distinct phases. The first phase is a (typically fast) clinging process in which the initially randomly oriented decision boundary gets very close to the low dimensional image manifold, which contains all the training examples. Next, there is a (typically slow) dimpling phase which creates shallow bulges in the decision boundary that move it to the correct side of the training examples. This framework provides a simple explanation for why adversarial examples exist, why their perturbations have such tiny norms, and why they look like random noise rather than like the target class. This explanation is also used to show that a network that was adversarially trained with incorrectly labeled images might still correctly classify most test images, and to show that the main effect of adversarial training is just to deepen the generated dimples in the decision boundary. Finally, we discuss and demonstrate the very different properties of on-manifold and off-manifold adversarial perturbations. We describe the results of numerous experiments which strongly support this new model, using both low dimensional synthetic datasets and high dimensional natural datasets.
-
 PatternBoost: Constructions in Mathematics with a Little Help from AIFrançois Charton, Jordan S. Ellenberg, Adam Zsolt Wagner, and Geordie Williamson2024
PatternBoost: Constructions in Mathematics with a Little Help from AIFrançois Charton, Jordan S. Ellenberg, Adam Zsolt Wagner, and Geordie Williamson2024We introduce PatternBoost, a flexible method for finding interesting constructions in mathematics. Our algorithm alternates between two phases. In the first “local” phase, a classical search algorithm is used to produce many desirable constructions. In the second “global” phase, a transformer neural network is trained on the best such constructions. Samples from the trained transformer are then used as seeds for the first phase, and the process is repeated. We give a detailed introduction to this technique, and discuss the results of its application to several problems in extremal combinatorics. The performance of PatternBoost varies across different problems, but there are many situations where its performance is quite impressive. Using our technique, we find the best known solutions to several long-standing problems, including the construction of a counterexample to a conjecture that had remained open for 30 years.
-
 Formal Mathematical Reasoning: A New Frontier in AIKaiyu Yang, Gabriel Poesia, Jingxuan He, Wenda Li, Kristin Lauter, Swarat Chaudhuri, and Dawn Song2024
Formal Mathematical Reasoning: A New Frontier in AIKaiyu Yang, Gabriel Poesia, Jingxuan He, Wenda Li, Kristin Lauter, Swarat Chaudhuri, and Dawn Song2024AI for Mathematics (AI4Math) is not only intriguing intellectually but also crucial for AI-driven discovery in science, engineering, and beyond. Extensive efforts on AI4Math have mirrored techniques in NLP, in particular, training large language models on carefully curated math datasets in text form. As a complementary yet less explored avenue, formal mathematical reasoning is grounded in formal systems such as proof assistants, which can verify the correctness of reasoning and provide automatic feedback. In this position paper, we advocate for formal mathematical reasoning and argue that it is indispensable for advancing AI4Math to the next level. In recent years, we have seen steady progress in using AI to perform formal reasoning, including core tasks such as theorem proving and autoformalization, as well as emerging applications such as verifiable generation of code and hardware designs. However, significant challenges remain to be solved for AI to truly master mathematics and achieve broader impact. We summarize existing progress, discuss open challenges, and envision critical milestones to measure future success. At this inflection point for formal mathematical reasoning, we call on the research community to come together to drive transformative advancements in this field.
-
 A Geometric Understanding of Deep LearningNa Lei, Dongsheng An, Yang Guo, Kehua Su, Shixia Liu, Zhongxuan Luo, Shing-Tung Yau, and Xianfeng GuEngineering, 2020
A Geometric Understanding of Deep LearningNa Lei, Dongsheng An, Yang Guo, Kehua Su, Shixia Liu, Zhongxuan Luo, Shing-Tung Yau, and Xianfeng GuEngineering, 2020This work introduces an optimal transportation (OT) view of generative adversarial networks (GANs). Natural datasets have intrinsic patterns, which can be summarized as the manifold distribution principle: the distribution of a class of data is close to a low-dimensional manifold. GANs mainly accomplish two tasks: manifold learning and probability distribution transformation. The latter can be carried out using the classical OT method. From the OT perspective, the generator computes the OT map, while the discriminator computes the Wasserstein distance between the generated data distribution and the real data distribution; both can be reduced to a convex geometric optimization process. Furthermore, OT theory discovers the intrinsic collaborative—instead of competitive—relation between the generator and the discriminator, and the fundamental reason for mode collapse. We also propose a novel generative model, which uses an autoencoder (AE) for manifold learning and OT map for probability distribution transformation. This AE–OT model improves the theoretical rigor and transparency, as well as the computational stability and efficiency; in particular, it eliminates the mode collapse. The experimental results validate our hypothesis, and demonstrate the advantages of our proposed model.
-
 The Modern Mathematics of Deep LearningJulius Berner, Philipp Grohs, Gitta Kutyniok, and Philipp PetersenDec 2022
The Modern Mathematics of Deep LearningJulius Berner, Philipp Grohs, Gitta Kutyniok, and Philipp PetersenDec 2022We describe the new field of mathematical analysis of deep learning. This field emerged around a list of research questions that were not answered within the classical framework of learning theory. These questions concern: the outstanding generalization power of overparametrized neural networks, the role of depth in deep architectures, the apparent absence of the curse of dimensionality, the surprisingly successful optimization performance despite the non-convexity of the problem, understanding what features are learned, why deep architectures perform exceptionally well in physical problems, and which fine aspects of an architecture affect the behavior of a learning task in which way. We present an overview of modern approaches that yield partial answers to these questions. For selected approaches, we describe the main ideas in more detail.
-
 Topos and Stacks of Deep Neural NetworksJean-Claude Belfiore, and Daniel BennequinDec 2022
Topos and Stacks of Deep Neural NetworksJean-Claude Belfiore, and Daniel BennequinDec 2022Every known artificial deep neural network (DNN) corresponds to an object in a canonical Grothendieck’s topos; its learning dynamic corresponds to a flow of morphisms in this topos. Invariance structures in the layers (like CNNs or LSTMs) correspond to Giraud’s stacks. This invariance is supposed to be responsible of the generalization property, that is extrapolation from learning data under constraints. The fibers represent pre-semantic categories (Culioli, Thom), over which artificial languages are defined, with internal logics, intuitionist, classical or linear (Girard). Semantic functioning of a network is its ability to express theories in such a language for answering questions in output about input data. Quantities and spaces of semantic information are defined by analogy with the homological interpretation of Shannon’s entropy of P.Baudot and D.Bennequin in 2015). They generalize the measures found by Carnap and Bar-Hillel (1952). Amazingly, the above semantical structures are classified by geometric fibrant objects in a closed model category of Quillen, then they give rise to homotopical invariants of DNNs and of their semantic functioning. Intentional type theories (Martin-Loef) organize these objects and fibrations between them. Information contents and exchanges are analyzed by Grothendieck’s derivators.
-
 Geometry of DataParvaneh Joharinad, and Jürgen JostDec 2022
Geometry of DataParvaneh Joharinad, and Jürgen JostDec 2022Topological data analysis asks when balls in a metric space (X,d) intersect. Geometric data analysis asks how much balls have to be enlarged to intersect. We connect this principle to the traditional core geometric concept of curvature. This enables us, on one hand, to reconceptualize curvature and link it to the geometric notion of hyperconvexity. On the other hand, we can then also understand methods of topological data analysis from a geometric perspective.
-
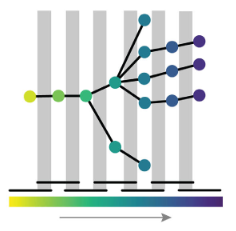 The shape of things to come: Topological data analysis and biology, from molecules to organismsErik J. Amézquita, Michelle Y. Quigley, Tim Ophelders, Elizabeth Munch, and Daniel H. ChitwoodDevelopmental Dynamics, Dec 2020
The shape of things to come: Topological data analysis and biology, from molecules to organismsErik J. Amézquita, Michelle Y. Quigley, Tim Ophelders, Elizabeth Munch, and Daniel H. ChitwoodDevelopmental Dynamics, Dec 2020Abstract Shape is data and data is shape. Biologists are accustomed to thinking about how the shape of biomolecules, cells, tissues, and organisms arise from the effects of genetics, development, and the environment. Less often do we consider that data itself has shape and structure, or that it is possible to measure the shape of data and analyze it. Here, we review applications of topological data analysis (TDA) to biology in a way accessible to biologists and applied mathematicians alike. TDA uses principles from algebraic topology to comprehensively measure shape in data sets. Using a function that relates the similarity of data points to each other, we can monitor the evolution of topological features—connected components, loops, and voids. This evolution, a topological signature, concisely summarizes large, complex data sets. We first provide a TDA primer for biologists before exploring the use of TDA across biological sub-disciplines, spanning structural biology, molecular biology, evolution, and development. We end by comparing and contrasting different TDA approaches and the potential for their use in biology. The vision of TDA, that data are shape and shape is data, will be relevant as biology transitions into a data-driven era where the meaningful interpretation of large data sets is a limiting factor.
-
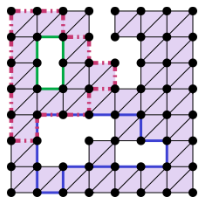 A User’s Guide to Topological Data AnalysisElizabeth MunchJournal of Learning Analytics, Jul 2017
A User’s Guide to Topological Data AnalysisElizabeth MunchJournal of Learning Analytics, Jul 2017Topological data analysis (TDA) is a collection of powerful tools that can quantify shape and structure in data in order to answer questions from the data’s domain. This is done by representing some aspect of the structure of the data in a simplified topological signature. In this article, we introduce two of the most commonly used topological signatures. First, the persistence diagram represents loops and holes in the space by considering connectivity of the data points for a continuum of values rather than a single fixed value. The second topological signature, the mapper graph, returns a 1-dimensional structure representing the shape of the data, and is particularly good for exploration and visualization of the data. While these techniques are based on very sophisticated mathematics, the current ubiquity of available software means that these tools are more accessible than ever to be applied to data by researchers in education and learning, as well as all domain scientists.
-
 Advancing mathematics by guiding human intuition with AIAlex Davies, Petar Veličković, Lars Buesing, Sam Blackwell, Daniel Zheng, Nenad Tomašev, Richard Tanburn, Peter Battaglia, and 6 more authorsNature, Jul 2021
Advancing mathematics by guiding human intuition with AIAlex Davies, Petar Veličković, Lars Buesing, Sam Blackwell, Daniel Zheng, Nenad Tomašev, Richard Tanburn, Peter Battaglia, and 6 more authorsNature, Jul 2021The practice of mathematics involves discovering patterns and using these to formulate and prove conjectures, resulting in theorems. Since the 1960s, mathematicians have used computers to assist in the discovery of patterns and formulation of conjectures1, most famously in the Birch and Swinnerton-Dyer conjecture2, a Millennium Prize Problem3. Here we provide examples of new fundamental results in pure mathematics that have been discovered with the assistance of machine learning—demonstrating a method by which machine learning can aid mathematicians in discovering new conjectures and theorems. We propose a process of using machine learning to discover potential patterns and relations between mathematical objects, understanding them with attribution techniques and using these observations to guide intuition and propose conjectures. We outline this machine-learning-guided framework and demonstrate its successful application to current research questions in distinct areas of pure mathematics, in each case showing how it led to meaningful mathematical contributions on important open problems: a new connection between the algebraic and geometric structure of knots, and a candidate algorithm predicted by the combinatorial invariance conjecture for symmetric groups. Our work may serve as a model for collaboration between the fields of mathematics and artificial intelligence (AI) that can achieve surprising results by leveraging the respective strengths of mathematicians and machine learning.